thesemi3d
Sep.1,2018: Most browsers (including Chrome and IE) have disabled Java and hence it is impossible to run Java applets in these browsers.   However, some browsers still  have Java enabled, such as Safari.   I use Safari on Macbook to run the applets from this site.  I bring my MacBook to classroom to visually demonstrate concepts with applet simulation in Safari.  CRW

Java updates (ver.7 and ver.8) and the applet problem:  The Java security settings in the recent (2014 & 2015) Java updates block the applets from running.  Follow this link to resolve it (set security level at high).  Add 'http://jas.eng.buffalo.edu' in your 'Exception Site List' of the Java control panel which is part of the Windows Control Panel. This will let your Windows OS allow the applets originating from jas.eng.buffalo.edu to run in your computer.   If you have the  local version license, having purchased the Semiconductor Applet local version, and would like to run the applets from your own computer, then add 'file:///' in the 'Exception Site List' of the Java control panel.  This will allow the applets from your own harddrive or from CD to run.  Mac users, please follow this link.

A picture is worth a thousand words. An animated picture is a thousand pictures.  An interactive animated picture with ability to change parameters is worth a thousand animations.  So, we  may be able to use an animated interactive visual applet to show a mathematical equation.  We attempted to represent some semiconductor equations with the interactive visual applets.

infoThe Semiconductor Applet Service website first came into service in 1996.
infoPapers describing the development of the semiconductor applets:
Bloch sphere model for two-qubit pure states:  I recently developed a Bloch sphere model for two-qubit pure states to make it work like the single-qubit Bloch sphere (full article link). For single qubits, Bloch sphere is a very useful tool, representing a quantum state as a point on the sphere and a single qubit gate as a rotation.  A classical bit is just two points on this sphere (North pole for 0 and South pole for 1), while a quantum bit can be any point on the sphere (a different point is a different superposition of  |0> and |1>).  Even a single-qubit state displays this quantum superposition which allows quantum parallelism in computation.  So far there was no similar Bloch sphere model for two qubits. The simplest quantum system that manifests the other important quantum property, the quantum entanglement, is a two-qubit pure state:   pure state.  The two-qubit Bloch sphere model for a pure state has three unit spheres and a circle as follows:
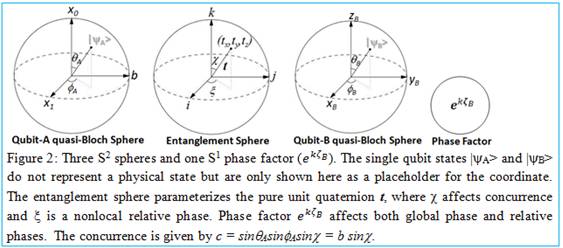
Bloch spheres
Bloch parameters
where i, j, k are the imaginary units of a quaternion and t is a unit pure-imaginary quaternion (paramterized by two angleschi, xi).   The maximally entangled states (MES) and the separable states can be shown on the qubit-A sphere and the entanglement sphere, for all possible qubit-B coordinates and phase factor, as follows:
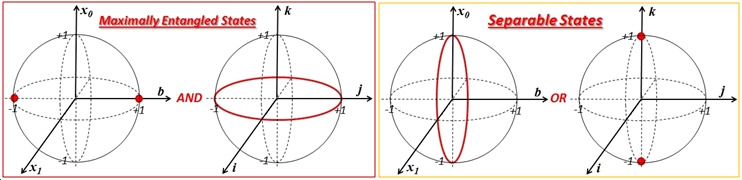
MES & Sperable
(April 2014)